“…like a Shakespearean sonnet that captures
the very essence of love, or a painting that brings
out the beauty of the human form that is far more
than just skin deep, Euler’s equation reaches down
into the very depths of existence.“
-Keith Devlin, Stanford University mathematics professor
Here it is, reaching deep, so deep put that ass to sleep:
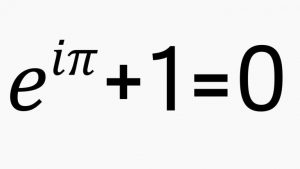
So…so…so beautiful. Books have been written about this equation (two pop-science books in the last two years: A Most Elegant Equation: Euler’s formula and the beauty of mathematics, David Strip (2017)–pretty good, and Euler’s Pioneering Equation: The most beautiful theorem in mathematics, Robin Wilson (2018)–bad). In 2004, a poll of readers by Physics World found Euler’s identity to be the “greatest equation ever.” EVER. Richard Feynman called Euler’s Identity “Our Jewl.”

And in 2014, a ridiculous study (who pays for this stuff?!) was conducted on the brains of sixteen mathematicians which found that the medial orbitofrontal cortex (emotional part of the brain, lights up for music, poetry, and pictures of bulldogs bathing on Instagram) lit up the most consistently for Euler’s identity than for any other formula. (Using science/technology to prove that we feel emotional about a mathematical formula…hmmmmmmmmmmmmmm010110110100100010101100.)
Origin story: Named after Leonhard Euler who was born in Switzerland in 1707:

He is considered the most prolific mathematician of all time, with 886 papers and books published. Most of this output came during the last twenty years of his life, when he was completely blind (ah, so he wasn’t winking, his body was shutting down, he went blind in his right eye in the late 1730s from an infection). In fact, his output was so extensive that the St. Petersburg Academy continued publishing his papers for thirty years after his death. Sort of like how I keep hearing new 2pac songs, even though he’s been dead for 22 years. Like this remix that came out four days ago:
Basically, Euler was a beast, a mathematician powerhouse. The French physicist François Arago described Euler:
“He calculated without any apparent effort, just as men breathe, as eagles sustain themselves in the air.”
Euler wrote about acoustics, musical harmonies, ship-building, prime numbers, yo mama, bridges, and more.
It is claimed that Euler’s identity appears first in his epoch-shattering work, Introductio in analysis infinitorum (1748):

What made this book “epoch-shattering” was that over the previous hundred years, since Descartes wrote about graphs, lines, and axes, there had been a gradual shift of mathematics from geometry towards algebra, and this book represented the scintillating climax when Euler defined the conic sections (ellipse, parabola, hyperbola) not as sections of a cone, but by using algebraic equations, beginning with this:
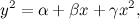
Despite revolutionizing the field of mathematics, changing the focus from geometry to algebra, Euler’s most popular and best-selling book was his pop-science book called Letters to a German Princess. This multiple volume work was an exposition that he created when he was asked to give simplifed science lessons to the Princess of Anhalt-Dessau.

The work was a collection of 200 letters that Euler wrote on topics ranging from gravity (gravity stops when I’m with you), light (you are the light of my life), astronomy (I’d rather have you than all of the stars), sound (I hear my heart beating when I’m with you), magnetism (I feel attracted to you like a…a magnet), the “electisation of men and animals, (uhhh)” and logic (what do you mean you’re busy all weekend?!)
Even though Euler’s identity is named after Euler, there is some debate on whether he was the first to produce the exact formula and to use it, since in Indroductio… he wrote down eix = cos x + i sin x but never took the final step (which is easy and simple) to write the identity above. In addition, Euler’s identity can be easily deduced from the work of Johann Bernoulli and Rodger Coates (who died in 1716 when Euler was 9 years old), but none of them did so. Who cares? They were busy. We’re all busy.
On the day Euler died (7th of September 1783) he was working on calculating the laws of the ascending motion of air balloons. He was dining with Mr. Lexell and his family, talking of Herschel’s planet (Uranus) and of the calculations which determine its orbit. Soon after, he was playing with his grandchild and drinking tea when he collapsed and died.

*
So why is Euler’s identity beautiful?
It connects five of the most fundamental constants of mathematics (0, 1, pie (3.141…), e (2.718…), and i (the imaginary unit of complex numbers))…
…using three fundamental operational symbols (addition, multiplication, and exponentiation), exactly once.
Also, the equation equals zero, which is common practice in several areas of mathematics.
But why is that beautiful?
Mathematics is the universal language that allows us to describe, with clarity and precision, the way the universe is structured and the way our reality works. Math links ideas and knowledge. It is often the foundation of innovations and allows us to fly planes, build skyscrapers, listen to music in the wilderness, post silly blog posts, and get inside someone’s crazy head who’s sweating butt naked in a chair on the other side of the planet. The more simple, and the higher number of things that an equation connects (a difficult paradox to balance), the more beauty.
So what is the mathematical definition of beauty? I think it’s this:
Connection and simplicity.
Subscribe below: